The Earth Radiant Energy Budget (ERBE) monthly albedo for the period 1986 to 1990 is shown above. Dark blue is low albedo and dark red high albedo.The red region in the southern hemisphere begins approximately in the 60S latitude range. In the northern hemisphere the higher albedo starts closer to 50N latitude.
Due to land mass in the NH and winter snow cover the season variation in albedo becomes significant near latitude 40N an peaks near latitude 60N. According to the Climate Data Information website, that change is roughly 0.3 or a 30% seasonal change. In the southern hemisphere the more critical region, 40S-60S is mainly ocean and there is little seasonal variation. Sea ice extent is part of the seasonal albedo change, but due to snow cover on land, small in comparison.
There is nothing particularly astonishing about snow and ice cover albedo being a major factor in climate change. It is after all the more likely reason Earth has the currently glacial/interglacial periods and why the 65N solar insolation variation in the Milankovitch cycles is considered the most likely trigger for deglaciation which would have a large impact on "surface" temperature, but not ocean energy necessarily. To get an estimate let's have a little thought experiment.
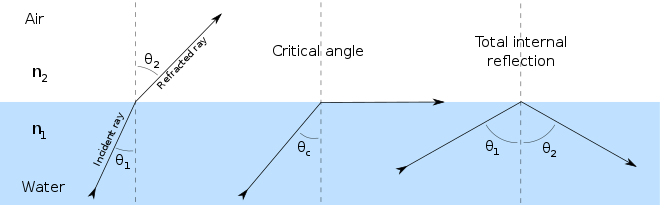
What if there were no land mass to hold the snow and ice at a higher altitude where it is harder to melt in season? With liquid oceans, the northern hemisphere albedo would be the same as the southern and if it weren't for the solar precessional cycle the surface albedo would still be high starting in the 60 to 90 latitude band at both poles. That is due to the reflection of solar insolation a the low angles of incidence off of water. If the oceans where perfectly calm, the surface albedo would be very close to the 25% to 30% range. For fresh water, the critical angle of reflection is close to 53 degrees.
This figure from the Wikipedia article on total internal reflection is a good illustration of what needs to be considered for a calm mirrored surface. Clouds scatter sunlight allowing solar insolation to be absorbed at lower angles and wave action increases the effective angle as well, increasing the effective critical angle to roughly 64 degrees or the Arctic circle latitudes. Since the oceans are capable of holding the most energy, a water world should have more total energy than a mixed land and ocean world and a higher average temperature. Assuming there is no precessional cycle and ignoring cloud albedo since it both reflects and scatters energy, you can estimate the amount of energy likely to be totally internally reflected in the oceans.
The average energy available at the surface from latitude 60S to 60N would vary from a peak of 100% at the equator to 50% at latitude 60. From horizon to horizon at the equator the insolation would vary from 0 near dawn and dust to 100% at noon. The total average insolation experiencing total internal reflection would be greater than 50% of the total insolation available while the average for the entire surface would be exactly 50% neglecting scattering and refraction in the atmosphere.
If you consider only the area likely to experience total internal reflection you would have a spherical cap.
The energy entering that spherical cap would be the 24/7/365 energy entering the oceans. You could change the rate of rotation, but the energy in would always be equal to the energy entering that cap area where it would be totally internally reflected and leave based on the thermal properties of the surface boundary.
For the cap, h would be the r*cos(60) and a r*sin(60), with r~6370km; a=6370*.866=5516km and h=3185km The area would be pi()*(a^2+h^2) or pi()[(5516)^2+(3185)^2]=62.3 million square kilometers.
With 1361 Wm-2 of solar insolation available the average insolation for the cap would be 0.866*1361=1178Wm-2. Correcting for average surface albedo of approximately 0.1, the approximate cap insolation would be 1060Wm-2 which with a total global area of 510msqkm would be ~130Wm-2 average energy totally internally reflected. If you allow for the actual area between 60S and 60N of ~440msqkm, the average insolation would be 150Wm-2. So you have a peak insolation of ~1060Wm-2, a diurnal average of 130-150 Wm-2 and a day only average of 260-300 Wm-2 that can be totally internal reflected versus a "global" average of 1361/4=340Wm-2 corrected for approximate "global" albedo or 0.30 results in 340*(1-.3)=238 Wm-2 for the full sphere. Using the higher estimate, 150/238=63% of the energy available is likely to be totally internally reflected or fully absorbed and 37% likely reflected.
The 37% reflected in this case would be equivalent to the geometric albedo. Geometric albedo depends on the type of surface. With water having a critical angle for total internal reflection it would also have a narrower range of angles for emission of energy. A more up/down orientation.
This table from the linked Wikipedia article lists estimated bond and geometric albedos for objects in our solar system. You will notice that there is considerable differences between Bond and Geometric albedo and that the quick estimate for Earth oceans agrees rather well with the table value.
If you assume that the entire surface of Earth can be estimated by using the Bond albedo but up to 63% of the energy is subject to total internal reflection requiring geometric albedo, you could have a significant error. In Earth's case .37/.30=1.23, up to a 23% error which could be called the liquid water greenhouse effect.



No comments:
Post a Comment