Imagine, if you will, a mushy ball orbiting our Sun. All we know about the new mushy ball is that it reflects some light, 30% to be exact. While we can't be sure, the mushy ball seems to have a temperature. Since we know the mushy ball's distance from the Sun and how much light it reflects, we can estimate that is should have a surface temperature, if a mushy ball has a surface, of about 255K degrees +/- a couple.
Joseph R. Genius, a renown scientist with the University of Psychedelic Experimentation determines that the mushy ball must have an interesting phenomena if it has a surface temperature greater than 255K +/- a couple. So J. R. Genius determines the total surface area of the mushy ball without bothering to determine if the mushy ball has a surface and proclaims that Mushy has a "surface" area of 4*pi*r^2 and that only half is illuminated, 2*pi*r^2 , but the actual area that is being shown upon is that of a flat disc, pi*r^2, so the average energy that impacts the surface is pi*r^2/4*pi*r^2 or 1/4 of the energy shown on a flat disc evenly distributed across the entire mushy surface.
Uri F. Kidding, also a renown scientist, says, "Okay Junior but what is the surface and why are you assuming uniform distribution of the energy? If Mushy is absorbing energy, that energy would tend to have a gradient from the warm equator to the colder poles."
"Because that is what S. R. Genius proposed in the peer reviewed literature."
And there you have it, the complete story of global warming. If planet Mushy can be constructed of any material and still have a "Greenhouse effect" then Jr. got some "splainin' to do.
"For the record I intuitively feel something is not right at a very fundamental level." Feelings are not science, but there is something in that simple comment lifted off a popular climate blog. Planet mushy is likely the key.
The Simple Radiant Model ( see here, here and here if curious) uses a simple cosine function. Latitudinal internal energy transfer would penetrate "walls". If the area of the "walls" are equal, then the transfer is simple. If the "walls" restrict transfer, then that complicates the situation. Since the radius of the Earth is ~6371 kilometers, a parallel cross-section of the Earth would be pi*[6371*cos(latitude)]^2. If the temperature or energy of the smalerl section is greater than the larger, energy would flow easily. If the temperature or energy of the larger section is greater, then there is a choke or bottle neck for energy flow. In equilibrium, the energy at any point would be balanced by the energy of all surrounding points. Since the Earth is not in true equilibrium, but a pseudo-steady state, then the energy flux from a point would have equal resistance to flow in all directions. Energy would be uniformly distributed and maintain that uniform distribution based on the resistance at each surrounding point.
Neither is the case with Earth, but planet Mushy can be forced to play that game. First, we have to straighten Mushy's axis, can't have that season variation between hemispheres. Now let's look at the latitude 60. That is where the cosine is 0.5 so the wall at 60 degree latitude would be 1/2 the area of the wall at the equator. The energy flowing from the equator through the 60 degree wall would be 1/2 the average value of the energy between 60N and 60S. If any energy is absorbed into the surface of Mushy, since the surface between 60N and 60S gains more energy than the latitudes outside 60N and 60S there will be energy flow through this 60 degree wall. If Mushy is in steady state and "conditionally" in equilibrium with the poles, i.e. 50% of the energy absorbed is flowing equally to the polar sections, the energy of the equatorial system would be in balance so that some percentage of the energy flow would be toward space and an equal amount of energy would be transferred to each pole. Energy flow would be equally distributed, internally and externally.
With this condition the energy flow through the equatorial wall would be zero, some percentage of the energy from 60S to the equator would be to space and some percentage into the 60S to pole section.
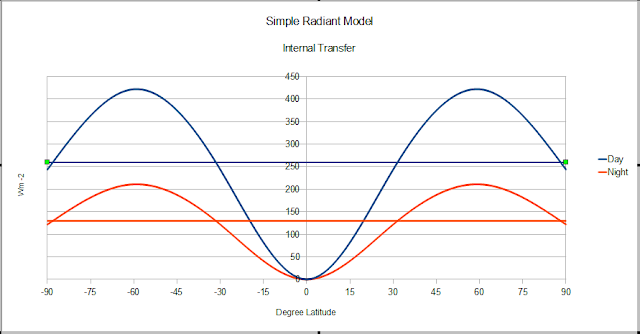
Internal transfer of energy would look something like this. Since Mushy is in a "conditional" equilibrium, both hemispheres have equal energy and both are losing equal amounts of energy to space. At the equator, the "wall" energy transfer is zero. The wall energy transfer peaks at 60 degrees latitude and at the poles, the mean internal energy transfer is lost to space. So as long as Mushy absorbs any energy it would have to transfer energy internally, UNLESS, the energy was equally distributed both internally and at the "surface". What Junior has to do is determine the mean "wall" transfer before Junior can determine the mean radiant impact, so he can determine the impact of any other changes to Mushy.
Now this considers the "walls" to be full cross sections. If the depth of the walls vary with latitude we would have a different shape to the curves. If the energy is unequally distributed we would have a different shape to the curves. So without any change in the "forcing" or energy provided, the physical internal composition of Mushy and the distribution of Mushy's energy would impact energy transfer. Unforced variability.
For temperature fans and as a double check, this the the temperature by latitude that the simple radiant model believes should be. 70% of 1361 Wm-2 is applied and distributed by the cosine of latitude. The "peak" temperature is equal to 4th root of the energy by latitude divided by the Stefan-Boltzmann constant 5.67e-8 minus 273.15 for conversion to C degrees, day is divided by two and average is just the simple average by latitude. The average for each is indicated in the legend. The simple model is not perfect, but -14.2 C is the temperature it believes is appropriate for a no greenhouse gas Earth. Since the Earth is a sphere, not a cylinder, this is a little higher than the simple average of -18C used in most cases.
The main point of the graph is between latitudes 45 and 65 where the Day and average values cross zero C degrees. Mushy, regardless of its composition would absorb considerable energy in the middle latitudes and up to roughly 70 degrees could be above zero degrees with 70% of the available solar energy of 1361Wm-2. If it takes longer than 12 hours for that absorbed energy to be transferred to the "surface" and then to space, Mushy would have a temperature greater than 255K +/- a couple.
One of the big caveats of course is albedo. If you assume Mushy is made of water than can be frozen, then the reflectivity would be higher, possibly as high as pure driven snow or it could be more interesting like, Mushy Ice, hence the name Mushy.
Just thought I would add this view of 10 degree walls.



No comments:
Post a Comment