By using the freezing point temperature of salt water and an estimated 50% relative humidity a Moisture Boundary Layer (MLB) can be defined to reduce the complexity of the energy budget of the Earth climate system. If the temperatures inside that "envelope" are stable and the atmosphere beyond that envelop is stable, a conditional equilibrium with a steady state internal energy flux equal to the steady state energy loss through the MBL layer can be assumed. That rate of energy flow is estimated at 118.1Wm-2. Now we can define a new boundary layer.
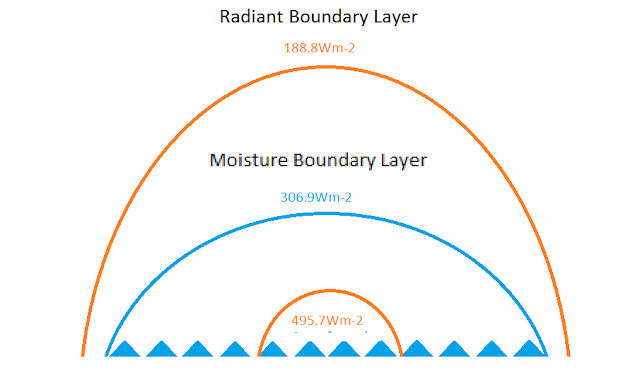
By using the 118.1Wm-2 as a reference and 306.9Wm-2 for the MBL boundary we can set our new boundary layer at 306.9-118.1=188.8Wm-2. For this layer to have that radiant energy flux, it would have a temperature of 240.2K degrees or about -32C degrees. This is sufficiently low that there should be no significant water vapor at this temperature.
For the MBL to be in equilibrium with this outer boundary layer, there would need to be an equal source internal to the MBL to balance this energy. Inside the MBL 294.25 was used as the Taverage which has an equivalent energy flux of 425Wm-2 or 118.1Wm-2 greater than the MBL shell. To balance the 240.2K boundary layer at 188.8Wm-2, the Tmax inside of the MBL could be the value of the MBL shell 306.9Wm-2 plus 188.8Wm-2 or 495.7Wm-2.
The drawing shows the Moisture Boundary Layer contained inside the Radiant Boundary Layer with the core energy source required to maintain the radiant sink at equilibrium. The latent heat of fusion of water is 334J/g and the latent heat of evaporation is 2257J/g both at sea level pressures. In side of the Radiant Boundary Layer all significant water phase changes would take place. If water is to be conserved and energy to be conserved, then the total energy change in the freezing, melting or evaporation of water would take place inside of the Radiant Boundary Layer. The volume enclosed in the Moisture Boundary Layer would change with the total energy available and the volume of ice outside of the MBL would vary proportional to the ratio 2257/334 = 6.76. For each gram of water evaporated, 6.76 grams of ice would have to form if the system is to remain in equilibrium. The volume of the MBL would expand or contract, but the energy flows at steady state would remain constant.
Those of you still awake may have noticed that the 306.9Wm-2 or 271.25K values of the MBL are based on the freezing temperature of salt water. Fresh water has a higher freezing point at 273.15K, 0C which has a radiant energy of 315.6Wm-2. Since the vast majority of liquid water on Earth is salt and the vast majority of frozen water is fresh, that would mean that conditions inside and outside of the MBL would vary depending of the ratio of salt water to fresh ice, that pesky 6.76 ratio that has to be considered. So for completeness, there should be a 273.15K secondary boundary layer.
This drawing shows the boundary layers with the pesky ice and snow layer. The enthalpy of fusion limits the temperature of the surfaces covered with fresh ice and snow to 0C at phase change. If there is ice and the temperature is below 0C, the ice only has a sensible impact on energy flux. At phase change though the ice would release or absorb 334J/g. In order for the MBL to expand or contract the enthalpy of fusion would have to be considered. ]
Now there are a few things interesting about the model so far. With the MBL layer at a stable 306.9Wm-2 and the total average energy Earth's surface estimated at 390Wm-2, the land surface outside of the MBL would have to provide 390-306.9=83.1Wm-2. Since the energy flux of the Radiant Boundary Layer is 188.8Wm-2, land surfaces inside of the RBL but outside of the MBL would have an average radiant energy or 188.8+83.1=271.9K degrees. Some of those still awake may be running to their calculators right now :)
The next installment

No comments:
Post a Comment